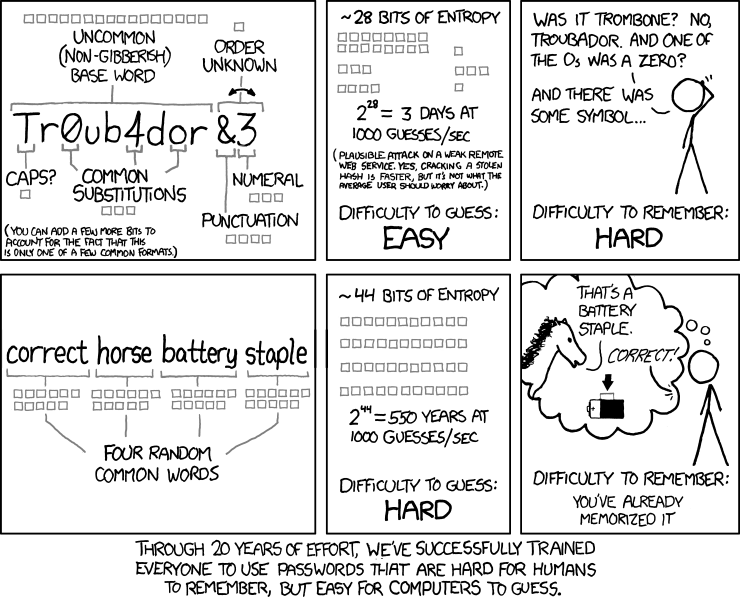
A while ago Randall Munroe posted a comic called "Password Strength":
This sparked a lot of debate on the Internet. Although the math seems right, after skimming through the discussions on the XKCD forums and on Stack Exchange, the whole thing has left me a bit skeptical, not as far as the mathematical matters go as much as on the assumptions on which the comic relies.
Scientific papers on security1 idiomatically define a so-called "attacker model", from which they derive assumptions about how someone will attempt to crack some particular computing system, in our case an arbitrary password-based authentication system. Now that we're done with the boring stuff, it's safe to say that assuming that any mildly experienced script kiddie will attempt a brute-force before a dictionary attack is completely nonsense.
Now, as per the comic and the previously stated analyses, a passphrase should at least in theory make a dictionary attack weaker, since it increases the word-level entropy, turning it into a brute-force attack at word-level. More exactly, for an alphabet $Sigma$ and a password $p$ of $l(p)$ elements from $Sigma$, the brute-forcing complexity is
$C(p) = left|{Sigma}right|^{l(p)}$
where $left|{cdot}right|$ denotes set cardinality.
I'll illustrate this by using the word count of the /usr/share/dict/words in
my distribution2:
% wc -l /usr/share/dict/words
99171 /usr/share/dict/words
The main difference between classical brute-forcing and a "brute-force dictionary" is that while the first uses as a basis a fixed alphabet (i.e. the printable ASCII charset plus-minus some Unicode) and a large exponent (i.e. the password length), the second relies solely on growing the alphabet's size.
So for word-level bruteforcing, we'll have:
$C_w(p) = left|{Sigma_w}right|^{l_w(p)} = 99171^4$
where $Sigma_w$ is a word-based alphabet and $l_w(p)$ is the number of words in a passphrase $p$.
In contrast, for a character-based alphabet $Sigma_c$ for which $left|{Sigma_c}right| = 26$, the password length yielding the equivalent complexity would have to be about $l_c(p) = 14.1243217044885998$, give or take a few decimal places.
One thing that I attempted to do was to find the "correct horse" passphrase's strength in relation to a smaller dictionary, which led me to the "tiny" dictionary from Openwall, of about 250 words. Interestingly enough, it seems that none of the words chosen for the passphrase given in the comic are in that dictionary, which would make words a pretty strong source of random words, assuming that the underlying random number generator is strong enough.
This is however only the beginning of a long, possibly neverending, intricate story. As passphrases become more common, I will venture to guess that "simply random" might not be enough and that some form of strong randomness will be required. For example, one might need to check that a given passphrase cannot be guessed by a Markov text generator based on the probability distribution inferred from, say, all the pages of Wikipedia. Natural language passphrases such as Assange's published password are thus becoming increasingly weak while password strength metrics vary more and more based on the attacker model.
[...] Take the following scenario for example: you're the only person who knows that your mother's name is Mary, leaving out, say, close people whom you trust; yet choosing "Mary" or even "MymomsnameisMary" as a password is a bad idea, as "Mary" is and has been so far a common name in the Western world, on the Internet and in the known Universe. Any common word in the dictionary is a bad idea, although more commonly-used random words should increase the password's security. [...]